هر آنچه باید درباره درخت مرکل و کاربردهای آن در بلاکچین بدانید
رالف مرکل دانشمند حوزه علوم کامپیوتر که به خاطر فعالیتش در زمینه رمزنگاری کلید عمومی معروف است در اوايل دهه 80 ميلادی، مفهوم کلی درخت مرکل را به جهان معرفی کرد.
درخت مرکل ساختاری است که به طور مؤثر برای تائید یکپارچگی دادهها در یک مجموعه استفاده میشود. جالبترین کاربرد درخت مرکل در زمینه شبکههای همتا به همتا به چشم میخورد؛ جایی که شرکتکنندگان باید اطلاعات را به اشتراک گذاشته و همچنین اعتبار اطلاعات را به طور مستقل مورد آزمایش قرار دهند.
ازآنجاییکه تابع هش در هسته ساختاری درخت مرکل قرار دارد؛ بد نیست برای درک بهتر ابتدا به مقاله تابع هش مراجعه کنید.
درخت مرکل چگونه کار میکند؟
تصور کنید میخواهید یک فایل با حجم بالا دانلود کنید. اگر این کار را با یک برنامه منبع باز انجام میدهید؛ باید بررسی کنید که آیا هش فایل دانلود شده با هش فایلی که توسط توسعهدهندگان به صورت عمومی منتشرشده است مطابقت دارد یا خیر . اگر پاسخ مثبت است؛ فایل دریافتی شما دقیقاً همان فایلی است که توسعهدهندگان در اختیار دارند.
مشکل زمانی به وجود میآید که این دو هش با یکدیگر یکسان نیستند. اگر هشها همسان نباشند؛ احتمالاً یا یک فایل مخرب و ویروسی که به ظاهر فایل موردنظر شماست طرف هستید و یا شاید هم فایل به درستی دانلود نشده باشد و در نتیجه کار نخواهد کرد. اگر مورد دوم باشد، شما مجبورید مجدداً فایل را دانلود کنید و امیدوار باشید که این بار فایل به صورت سالم دانلود شود.
اما آیا راهی وجود دارد که از دردسر دانلود مجدد یک فایل حجیم، در صورت اشکالات احتمالی خلاص شویم؟ خوشبختانه بله و درست همینجاست که درختان مرکل وارد داستان میشوند.
با یکی از این درختان، فایل شما به چندین بخش تقسیم میشود، مثلاً اگر حجم فایل 50 گیگ باشد؛ شما میتوانید آن را به صد بخش تقسیم کنید. بهطوریکه هر یک از آنها دارای حجم 0.5 گیگابایتی باشند؛ سپس بخش بخش اقدام به دانلود فایل کنید. در واقع این همان شیوهای است که در فایلهای تورنت مورد استفاده قرار میگیرد.
در این حالت منبع شما هش معروف به ریشه مرکل را در اختیار شما قرار میدهد. این هش نمایانگر هر بخش دادهای است که فایل شما را تشکیل میدهد؛ اما ریشه مرکل اعتبار سنجی دادهها را بسیار آسانتر میکند.
بیایید برای سادهتر شدن این موضوع از یک مثال ساده استفاده کنیم که در آن از یک فایل 8 گیگابایتی استفاده شده که به هشت بخش تقسیمشده است. بخشهای مختلف فایل از A تا H نامگذاری شدهاند. سپس هر بخش از یک تابع هش عبور داده میشود و هشت هش مختلف به دست میآید.

حالا قسمتهای مختلفی از یک پازل در اختیار ماست که همهچیز را کمی منطقیتر میکند. ما به هش فایلها و همه بخشهای فایل دسترسی داریم؛ بنابراین اگر یکی از بخشها دارای مشکل باشد؛ با مقایسه آن با فایل منبع به مشکل پی خواهیم برد. این طور نیست؟ احتمالاً؛ اما فراموش نکنید که این روش فوقالعاده ناکارآمد است. بهعنوانمثال اگر فایل دارای هزاران بخش باشد؛ آیا همچنان میشود که همه فایل را با هش مقایسه کرد و نتایج دقیقی به دست آورد؟ البته که نه!
ما در عوض میتوانیم هر جفت هش را گرفته و آنها را ترکیب کنیم و سپس آنها را با هم هش میکنیم؛ بنابراین ما هشهای hA + hB، hC + hD، hE + hF و hG + hH را داریم. در آخر به چهار هش میرسیم. سپس یک دور دیگر ترکیب کردن و هش کردن را با اینها انجام میدهیم تا به دو هش ختم شود و در آخر با همین روش، دو مورد باقیمانده را هش میکنیم تا به هش اصلی برسیم که ریشه مرکل (یا ریشه هش) نام دارد.
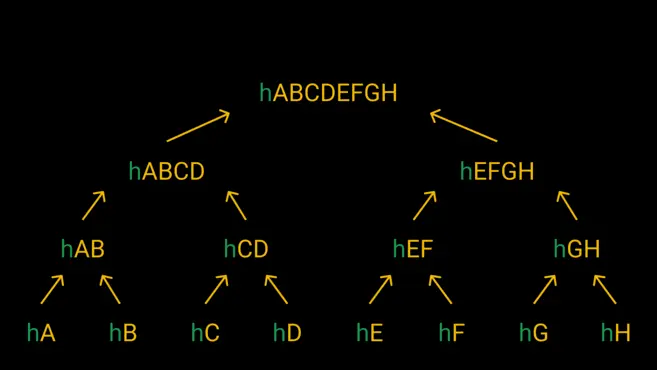
ساختار درخت مرکل شبیه به یک درخت وارونه است. در ردیف پایین، برگهایی است که برای تولید گرهها و درنهایت تولید ریشه ترکیبشدهاند.
حالا ما به ریشه مرکل دست پیدا کردیم که در واقع نماینده فایل دانلود شده ماست. در اینجا به سادگی میتوانیم این ریشه هش را با آنچه در فایل منبع ارائه شده مقایسه کنیم. اگر با یکدیگر مطابقت دارند که بسیار عالی! اما اگر هشها متفاوت باشد، میتوان مطمئن بود که دادهها دستکاریشدهاند. بهعبارتدیگر، یک یا چند بخش، هشی متفاوت ایجاد کردهاند؛ بنابراین هرگونه تغییر جزئی، ریشه مرکل کاملاً متفاوتی ایجاد میکند.
خوشبختانه، یک روش کاربردی برای بررسی و شناسایی بخشهای ناسالم یا اصطلاحا ّFaulty وجود دارد. به مثال بالا برمیگردیم:
فرض کنیم hE بخش دستکاریشده یا خراب این مجموعه باشد ولی ما این را نمیدانیم و میخواهیم پس از پیدا کردن بخش معیوب آن را مجدداً دانلود کنیم. برای پیدا کردن بخش معیوب باید مراحل زیر را پشت سر بگذاریم:
مرحله اول: باید از نزدیکترین قسمت به ریشه درخت شروع کنیم. برای شروع باید از یک peer یا همتا درخواست کنید که دو هش تولیدشده ریشه مرکل را در اختیار شما قرار دهد (hABCD و hEFGH). داده hABCD شما باید با داده فایل مطابقت داشته باشد. چرا؟ چون در قسمت زیر درخت (Subtree) داده hABCD هیچ خطایی رخ نداده است و همهچیز مطابق دادههای فایل است. پس باید در hEFGH به دنبال بخش ناسالم بگردیم.
مرحله دوم: زیر درختهای متصل به این هش را درخواست میکنیم یعنی هش hEF و hGH. آنها را با نسخه خود مقایسه میکنیم. hGH به نظر درست است پس زیر درختهای آن از اتهام ناسالم بودن، تبرئه میشوند. پس میدانیم که hEF بخش معیوب ما است و به همین خاطر به سراغ زیر درختهای آن میرویم.
مرحله سوم: در آخر، هشهای hE و hF را مقایسه میکنیم. در اینجاست که بخش معیوب خود را نشان میدهد و دیگر میدانیم که hE نادرست بوده بنابراین دوباره آن قسمت را دانلود میکنیم.
به طور خلاصه، یک درخت مرکل با تقسیم دادهها به بخشهای زیاد ایجاد میشود که پس از آن به طور مکرر هش شده و درنهایت ریشه مرکل ایجاد شود. سپس میتوان به درستی تائید کرد که آیا در قسمتی از دادهها اشتباهی رخ داده است؟
ریشههای مرکل در بیت کوین چه کاربردی دارند؟
درخت مرکل در بیت کوین و بسیاری از رمزارزها عنصری ضروری به شمار میروند. آنها یکی از اجزای جداییناپذیر در هر بلوکاند. شما میتوانید آنها را در بخش Header بلوکها پیدا کنید. برای به دست آوردن برگهای درختمان، از هش تراکنش (TXID) هر تراکنش درون بلوک استفاده میکنیم.
در واقع ریشه مرکل به منظور رسیدن به دو هدف مورد استفاده قرارگرفته است؛ استخراج رمزارزها و تائید تراکنشها.
استخراج یا ماینینگ
بلوک بیت کوین از دو بخش تشکیل شده است. بخش اول هدر بلوک Header block است، این بخش ظرفیت و سایز ثابتی دارد و فراداده (Metadata) بلوک در این بخش قرار دارد. بخش دوم لیستی از تراکنشها ظرفیت متغیر است و میزان آن بیشتر از بخش هدر است.
ماینرها برای تولید خروجی و استخراج یک بلوک معتبر، باید بارها و بارها داده را هش کنند. ممکن است این موضوع میلیاردها بار انجام شود تا بالاخره بلوک معتبر پیدا شود. با هر بار تلاش آنها یک عدد تصادفی را در هدر بلوک (nonce) تغییر میدهند تا یک خروجی متفاوت ایجاد کنند؛ اما بخشهای بسیاری از بلوکها به همان شکل باقی میمانند. ممکن است هزاران تراکنش وجود داشته باشد و کماکان باید هر بار آنها را هم هش کرد.
ریشه مرکل روند را بهطور فزایندهای ساده میکند. هنگامیکه فرایند استخراج شروع میشود؛ تمام تراکنشهای موردنظر ماینر در یک ردیف قرار میگیرد و یک درخت مرکل ساخته میشود. ریشه هش حاصلشده (32 بایت) در هدر بلوک قرار داده میشود. سپس، هنگام استخراج، بهجای هش کل بلوک، فقط باید هدر بلوک را هش نمود.
این روش عملی است چرا که آنچه توضیح دادهشده قابلیت دستکاری ندارد. به شکلی مؤثر همه تراکنشهای بلوک را در یک قالب فشرده خلاصه میشود. اینطور نیست که یک بلوک هدر معتبر پیدا شود و بعداً لیست تراکنشها دستکاری یا دچار تغییر شود، زیرا این امر باعث تغییر ریشه مرکل میشود. هنگامیکه بلوک به گرههای دیگر ارسال میشود؛ آنها ریشه را از لیست تراکنشها محاسبه میکنند و اگر با آنچه در هدر است مطابقت نداشته باشد؛ بلوک را موردپذیرش قرار نمیدهند.
تائید
ویژگی کاربردی جالب دیگر از ریشههای مرکل مربوط به کلاینتهای سبک (Light clients) است (گرههایی که کپی نسخه کامل بلاکچین را ندارند). اگر گره بیت کوین را اجرا میکنید ولی محدودیتها اجازه نمیدهد که نسخه کامل تراکنشهای بلاک را دانلود و آنها را هش کنید؛ میتوانید به سادگی از Merkle proof یا اثبات مرکل استفاده کنید.
این اثبات توسط یک گره کامل (Full node) ارائه شده است و ثابت میکند که تراکنش شما در یک بلوک خاص قرار دارد. به این روش معمولاً عنوان تائید پرداخت ساده یا SPV دادهشده است و توسط ساتوشی ناکاموتو در وایتپیپر بیت کوین شرح دادهشده است.
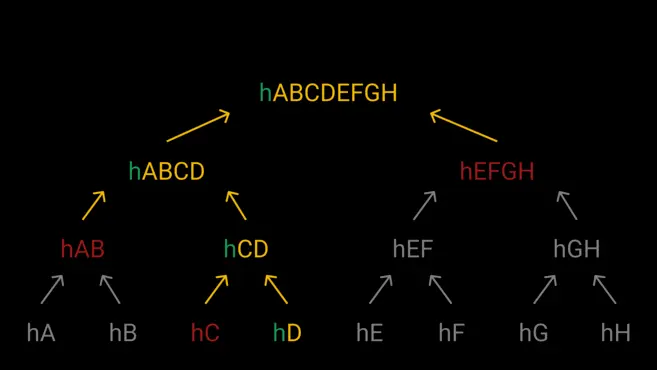
فرض کنید که میخواهیم اطلاعات مربوط به تراکنشی را که TXID آن hD است را بدانیم. اگر hC در اختیار ما قرار بگیرد، میتوان روی hCD کار کنیم. سپس، برای محاسبه (HAB) به hABCD نیاز داریم؛ و سرانجام با hEFGH میتوانیم بررسی کنیم که آیا ریشه مرکل حاصلشده با هدر بلوک مطابقت دارد یا خیر. مطابقت داشتن ریشه مرکل حاصلشده با هدر بلوک، اثبات این است که تراکنش در بلوک موجود است. لازم به ذکر است که ایجاد یک هش مشابه با دادههای مختلف تقریباً غیرممکن است.
در مثال بالا ما تنها سه بار باید فرایند هش را انجام بدهیم. این در حالی است که بدون اثبات مرکل (Merkle proof)، لازم بود تا این کار را هفت بار انجام دهیم. از آنجا که امروزه بلوکها شامل هزاران تراکنش هستند؛ استفاده از اثبات مرکل در زمان و منابع محاسباتی ما صرفهجویی چشمگیری میکند.
سخن آخر
درختان مرکل جای خود را در طیف وسیعی از برنامههای علوم رایانه تثبیت کردهاند و همانطور که دیدیم؛ آنها در بلاکچین نیز بسیار ارزشمند هستند. در سیستمهای توزیعشده، درختان مرکل امکان تائید آسان اطلاعات را بدون پر کردن شبکه با دادههای غیرضروری فراهم میکنند.
بدون درختان مرکل و ریشههای مرکل، بیت کوین و سایر ارزهای دیجیتال به اندازه امروز مقرونبهصرفه نبودند. اگرچه Light client ها در بحث حریم خصوصی و امنیتی حرفی برای گفتن ندارند؛ ولی با امکان اثبات مرکل (Merkle proof) کاربران قادر شدهاند تا وجود تراکنش خود در یک بلوک را با کمترین هزینه بررسی کنند.






